Question

Find KH. A. 3 and 3/7, B. 4 and 2/3, C. 10 and 1/2, or D. 21

Answer 1

Take into account that triangles FGH and GKJ are similar. Then, you can write the following equivalence between the lengths of similar sides:

`(GH)/(GK)=(FG)/(JG)`

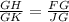
where,

GH = ?

GK = 6

FG = 7 + 4 = 11

JG = 4

Solve for GH, replace the values of the other parameters and simplify:

`\begin{gathered} GH=((FG)/(JG))\cdot GK \\ GH=((11)/(4))\cdot6 \\ GH=(66)/(4)=(33)/(2) \end{gathered}`

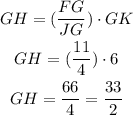
Now, take into account that:

GH = GK + KH

Solve for KH, replace the values of GH and GK and simplify:

`\begin{gathered} KH=GH-GK \\ KH=(33)/(2)-6 \\ KH=(33-12)/(2)=(21)/(2)=10(1)/(2) \end{gathered}`

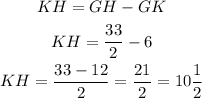
Hence, the lngth of KH is 10 1/2