Given,
The height of the cliff, h=65 m
The extension length of the cliff, i.e., the range of the jump, R=25 m
From the equation of motion, the height of the jump is given by,
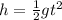
Where g is the acceleration due to gravity and t is the time of flight of the diver.
On substituting the known values,
![\begin{gathered} 65=(1)/(2)*9.8* t^2 \\ t=\sqrt[]{(2*65)/(9.8)} \\ =3.64\text{ s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/high-school/pbbnpeqmgvg4zlx9aci9baikqpnw5ltr7z.png)
Thus the time of flight of the diver is 3.64 s
The initial velocity of the diver is given by the equation,
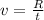
On substituting the known values,
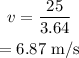
Thus the diver has to jump with an initial velocity of 6.87 m/s