Question

Math 8th grander, please help us

Answer 1

The first thing we have to see is that exercise (c) is given as follows

`(c)_{}\to(-4)/(f(k))`

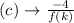
From (e) we know:

`f(k)=-4k+7`

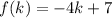
So we replace f(k) of the (e) part on the (c) part as follows:

`f(k)=(-4)/((-4k+7))`

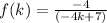
Now we must find the value of x the function F (k) is not defined. This value is given when the denominator of the function gives 0 since the function would be indeterminate then:

`\begin{gathered} -4k+7=0 \\ -4k=-7 \\ k=(7)/(4) \end{gathered}`

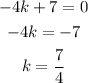
The domain of this function is indeterminate for k = 7/4 and this value is the one that must be excluded from the domain

All functions have a domain and a range. The domain of a function is all the values that the function can take along the k-axis and the range on the f(k)-axis.