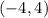3. X = y -8 -X - y = 0 Step 1 Step 2 Step 3 Step 4 Fly-8) - y = 0 Solve for Y Solve for X Give Coordinate

Question

asked Jan 2, 2023 198k views

1 Answer

Christoph Dietze · Answer 1 · 2023-01-07T17:25:12+0000

The given system is

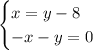
$\begin{cases}x=y-8 \\ -x-y=0\end{cases}$

Step 1: We combine the first equation with the second one

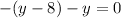
Step 2: Solve for y.

First, we use the distributive property, then we combine like terms

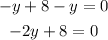
$\begin{gathered} -y+8-y=0 \\ -2y+8=0 \end{gathered}$

Now, we subtract 8 from each side

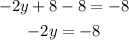
$\begin{gathered} -2y+8-8=-8 \\ -2y=-8 \end{gathered}$

Then, we divide the equation by -2.

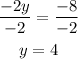
$\begin{gathered} (-2y)/(-2)=(-8)/(-2) \\ y=4 \end{gathered}$

Step 3: we solve for x.

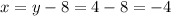
Step 4: Give Coordinate, we just have to write down the solutions as coordinates.