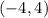The given system is
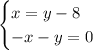
Step 1: We combine the first equation with the second one
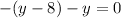
Step 2: Solve for y.
First, we use the distributive property, then we combine like terms
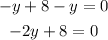
Now, we subtract 8 from each side
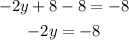
Then, we divide the equation by -2.
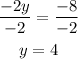
Step 3: we solve for x.
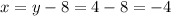
Step 4: Give Coordinate, we just have to write down the solutions as coordinates.