Question

A local water park has two types of season passes. Plan A costs a one-time fee of $139 for admission plus $8for parking every trip. Plan B costs a one-time fee of $43 for parking plus $24 for admission every trip. Howmany visits must a person make for plan A and plan B to be equal in value?O 12O 3O 5O 6

Answer 1

So,

We could state the following equations:

Let "x" be the number of visits of a person in a trip, and let "y" be the cost.

For plan A, we could write:

`y=8x+139`

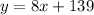
For plan B, we could write:

`y=24x+43`

To find the number of visits that a person must make for plan A and plan B to be in equal value, we should equal the equations of both plans, and solve the resulting equation for x, as follows:

`\begin{gathered} 8x+139=24x+43 \\ 139-43=24x-8x \\ 96=16x \\ x=(96)/(16)=6 \end{gathered}`

Therefore, x=6.

So, if a person makes 6 visits, plan A and plan B would be in equal value.