Question

Find the area of the triangle with a = 19, b = 14, c = 19. Round to the nearest tenth.

Answer 1

In order to find the area of a triangle with 3 sides, we use the Heron's formula which says if a, b, and c are the three sides of a triangle, then its area is,

`\begin{gathered} Area=A=\sqrt[]{S(S-a)(S-b)(S-c)} \\ S=\text{Semiperimeter}=(a+b+c)/(2) \end{gathered}`

Given a triangle with a = 19, b = 14, c = 19, the area is as shown below:

`\begin{gathered} S=(19+14+19)/(2) \\ S=(52)/(2) \\ S=26 \end{gathered}`
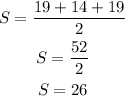
`\begin{gathered} A=\sqrt[]{S(S-a)(S-b)(S-c)} \\ A=\sqrt[]{26(26-19)(26-14)(26-19)} \\ A=\sqrt[]{26(7)(12)(7)} \\ A=\sqrt[]{15288} \\ A=123.6447 \\ A=123.6(\text{nearest tenth)} \end{gathered}`

Hence, the area of the triangle is 123.6 square unit correct to the nearest tenth