The ratios that they can make a proportion will be that which
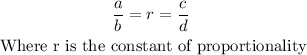
So, you have
First ratios
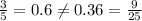
Second ratios
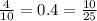
Third ratios
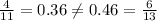
Fourth ratios
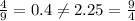
Then, as you can see, the ratios that share a constant of proportionality and that make a proportion are
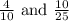
Therefore, that is the correct answer.