Diane purchased 7 pens
Step-by-step explanation:
Cost of one pen = 60 cents = 60/100 = $0.60
Cost of one pencil = 40 cents =40/100 = $0.40
let the number of pens bought = x
let the number of pencils bought = y
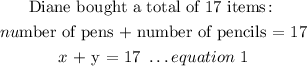
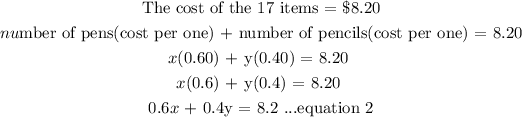
combining both equatons:
x + y = 17 ....equation 1
0.6x + 0.4y = 8.2 ...equation 2
using substitution method:
let's make x the subject of formula
from equation 1:
x = 17 - y ....equation 3
substitute for x in equation 2:
0.6(17 - y) + 0.4y = 8.2
10.2 - 0.6y + 0.4y = 8.2
collect like terms:
10.2 - 0.2y = 8.2
10.2 - 8.2 = 0.2y
2 = 0.2y
y = 2/0.2
y = 10
substitute for y in equation 1:
x + 10 = 17
x = 17 - 10
x = 7
x = number of pens = 7
Hence, Diane purchased 7 pens