Question

The office supply superstore sell pens for 60 cents each and pencils for 40 cents each. Diane purchased a total of 17 items (pens and pencils) for $8.20. How many pens did Diane purchase?

Answer 1

Diane purchased 7 pens

Step-by-step explanation:

Cost of one pen = 60 cents = 60/100 = $0.60

Cost of one pencil = 40 cents =40/100 = $0.40

let the number of pens bought = x

let the number of pencils bought = y

`\begin{gathered} \text{Diane bought a total of 17 items}\colon \\ nu\text{mber of pens + number of pencils = 17} \\ x\text{ + y = 17 }\ldots equation\text{ 1} \end{gathered}`
`\begin{gathered} \text{The cost of the 17 items = \$8.20} \\ nu\text{mber of pens(cost per one) + number of pencils(cost per one) = 8.20} \\ x(0.60)\text{ + y(0.40) = 8.20 } \\ x(0.6)\text{ + y(0.4) = 8.20 } \\ 0.6x\text{ + 0.4y = 8.2 ...equation 2} \end{gathered}`

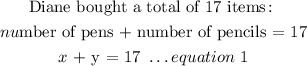
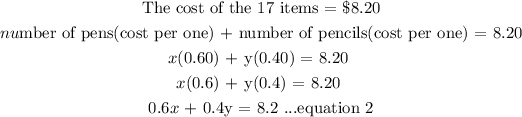
combining both equatons:

x + y = 17 ....equation 1

0.6x + 0.4y = 8.2 ...equation 2

using substitution method:

let's make x the subject of formula

from equation 1:

x = 17 - y ....equation 3

substitute for x in equation 2:

0.6(17 - y) + 0.4y = 8.2

10.2 - 0.6y + 0.4y = 8.2

collect like terms:

10.2 - 0.2y = 8.2

10.2 - 8.2 = 0.2y

2 = 0.2y

y = 2/0.2

y = 10

substitute for y in equation 1:

x + 10 = 17

x = 17 - 10

x = 7

x = number of pens = 7

Hence, Diane purchased 7 pens