The question
![\sqrt[]{3}+i](https://img.qammunity.org/2023/formulas/mathematics/college/hqnfre6o1n9ajylv57j9qozgokmof2aeca.png)
is written in the standard rectangular form:
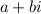
To write in polar form, we must write it in the format
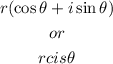
To find r, we can use the formula
![\begin{gathered} r=\sqrt[]{a^2+b^2} \\ \text{where} \\ a=\sqrt[]{3} \\ b=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/p190wceuq54cvajoq3i2scvulyja03rsy0.png)
Solving, we have
![\begin{gathered} r=\sqrt[]{(\sqrt[]{3})^2+1^2} \\ r=\sqrt[]{3+1}=\sqrt[]{4} \\ r=2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/cqhqyq577n04cri0jafyqurj7g3hxi0lcg.png)
To find θ, we use
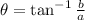
Substituting the values, we have
![\begin{gathered} \theta=\tan ^(-1)\frac{1}{\sqrt[]{3}} \\ \theta=30^(\circ) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r2q2fiypmxe1fpereamg3hmtzsl2nzf34h.png)
In polar form,
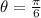
Note that since a and b are positive, the angle is in the first quadrant. Hence, we use the angle as is.
Therefore, we have the answer to be
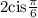
OPTION A is correct.