Question

57Convert4cis 3 to rectangular form.O A.-2 – 2/31OB. -2 + 2/31O C. 2 - 2/31OD. 2 + 2/31

Answer 1

The question

`\sqrt[]{3}+i`

is written in the standard rectangular form:

`a+bi`

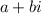
To write in polar form, we must write it in the format

`\begin{gathered} r(\cos \theta+i\sin \theta) \\ or \\ rcis\theta \end{gathered}`

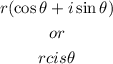
To find r, we can use the formula

`\begin{gathered} r=\sqrt[]{a^2+b^2} \\ \text{where} \\ a=\sqrt[]{3} \\ b=1 \end{gathered}`

Solving, we have

`\begin{gathered} r=\sqrt[]{(\sqrt[]{3})^2+1^2} \\ r=\sqrt[]{3+1}=\sqrt[]{4} \\ r=2 \end{gathered}`

To find θ, we use

`\theta=\tan ^(-1)(b)/(a)`

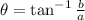
Substituting the values, we have

`\begin{gathered} \theta=\tan ^(-1)\frac{1}{\sqrt[]{3}} \\ \theta=30^(\circ) \end{gathered}`

In polar form,

`\theta=(\pi)/(6)`

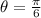
Note that since a and b are positive, the angle is in the first quadrant. Hence, we use the angle as is.

Therefore, we have the answer to be

`2\text{cis}(\pi)/(6)`

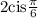
OPTION A is correct.