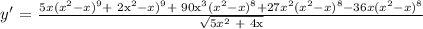The given expression is
= (x²-x)^9(√5x²+4x)
We would differentiate it by applying the product rule. It is expressed as
(fg)' = f'g + fg'
Let f = (x²-x)^9
Let g = (√5x²+4x)
f' = 9(2x - 1)(x²-x)^8
g = (√5x²+4x) = (5x²+4x)^1/2
g' = 1/2(10x + 4)(√5x²+4x)^-1/2
g' = (10x + 4)/2(√5x²+4x)
g' = (5x + 2)/(√5x²+4x)
By applying the rule, it becomes
9(2x - 1)(x²-x)^8 * (√5x²+4x) + (x²-x)^9 * (5x + 2)/(√5x²+4x)
By simplifying,