Solution
- The question asks us which of the options has the domain specified below:

- The domain just simply refers to all the possible values of x the function can take without being undefined.
- We have been told that the domain is any x value that is greater than or equal to 8. This means that the domain contains values
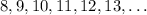
- Thus, we simply need to test each option with a number NOT in the range of numbers given above and see if the result of f(x) gives us a defined number. If it does, then, the function has a domain wider than x ≥ 8. However, if the function becomes undefined for all real numbers, then the function has a domain of exactly x ≥ 8.
- These operations are done below:
![\begin{gathered} \text{ For these tests, we can use }x=0\text{ since }x=0\text{ is not in the range }x\ge8 \\ \\ \text{Option 1:} \\ f(x)=\sqrt[]{x-8}+1 \\ f(0)=\sqrt[]{0-8}+1 \\ f(0)=\sqrt[]{-8}+1 \\ \text{ Since }\sqrt[]{-8}\text{ is not a real number, this function is the correct answer} \\ \\ \\ \text{Thus,} \\ f(x)=\sqrt[]{x-8}+1\text{ is the Answer} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ntqljj6qoaduyw60et0cpjyh7hooytl6yk.png)
- After testing just one value, we have been able to find an option that satisfies our condition
Final Answer
The final answer is
![f(x)=\sqrt[]{x-8}+1\text{ (OPTION 1)}](https://img.qammunity.org/2023/formulas/mathematics/college/yz4gym8nx02ym8kqo5kx6y6im8gpe91lzb.png)