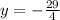To obtain the vertex of the parabola, we are going to re-write the given parabola equation into its vertex form.
The vertex form of a parabola is given as:
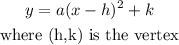
Thus, by completing the square of the given parabola equation, we have:
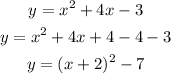
Comapring this equation with the vertex form of a parabola;
Hence, the vertex of the parabola is:
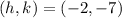
The focus of a parabola is at the point;
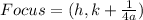
The parabola obtained opens up. An alternative equation for a parabola that opens up is:
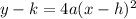
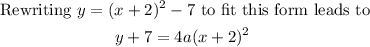
We must find the value of a that makes the equation true at any point (x,y).
Suppose x=1;
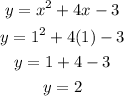
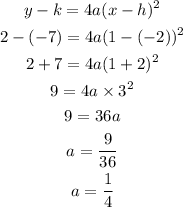
Hence, the focus of the parabola is:
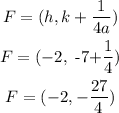
The directrix is: