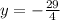Question

Identify the vertex the focus and the directrix of the parabola with the given equation: y=x2+4x-3

Answer 1

To obtain the vertex of the parabola, we are going to re-write the given parabola equation into its vertex form.

The vertex form of a parabola is given as:

`\begin{gathered} y=a(x-h)^2+k \\ \text{where (h,k) is the vertex} \end{gathered}`

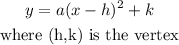
Thus, by completing the square of the given parabola equation, we have:

`\begin{gathered} y=x^2+4x-3 \\ y=x^2+4x+4-4-3 \\ y=(x+2)^2-7 \end{gathered}`

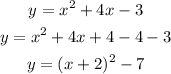
Comapring this equation with the vertex form of a parabola;

Hence, the vertex of the parabola is:

`(h,k)=(-2,-7)`

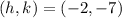
The focus of a parabola is at the point;

`Focus=(h,k+(1)/(4a))`

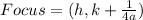
The parabola obtained opens up. An alternative equation for a parabola that opens up is:

`y-k=4a(x-h)^2`
`\begin{gathered} \text{ Rewriting }y=(x+2)^2-7\text{ to fit this form leads to} \\ y+7=4a(x+2)^2 \end{gathered}`

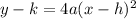
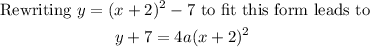
We must find the value of a that makes the equation true at any point (x,y).

Suppose x=1;

`\begin{gathered} y=x^2+4x-3 \\ y=1^2+4(1)-3 \\ y=1+4-3 \\ y=2 \end{gathered}`
`\begin{gathered} y-k=4a(x-h)^2 \\ 2-(-7)=4a(1-(-2))^2 \\ 2+7=4a(1+2)^2 \\ 9=4a*3^2 \\ 9=36a \\ a=(9)/(36) \\ a=(1)/(4) \end{gathered}`

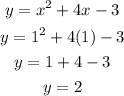
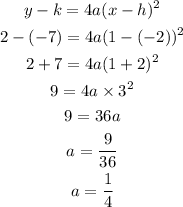
Hence, the focus of the parabola is:

`\begin{gathered} F=(h,k+(1)/(4a)) \\ F=(-2,\text{ -7+}(1)/(4)) \\ F=(-2,-(27)/(4)) \end{gathered}`

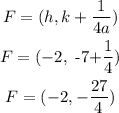
The directrix is:

`y=-(29)/(4)`