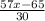Question

Addition and subtraction of algebraic expressions(9x - 1)/6 + (2x -10)/5

Answer 1

To solve this question, follow the steps below.

Step 01: Find the LCM of 5 and 6 (denomitators).

5, 6 | 2

5, 3 | 3

5, 1 | 5

1, 1

The LCM is 2*3*5 = 30

Step 02: Rewrite the fractions using 30 as the denominator.

To do it, divide 30 by the original denominator and multiply the result by the numerator.

`(5\cdot(9x-1))/(30)+(6\cdot(2x-10))/(30)`

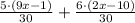
Step 03: Solve the expression.

First, since the fractions have the same denominator, you can write them using only one denominator:

`(5\cdot(9x-1)+6\cdot(2x-10))/(30)`

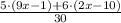
Now, remove the parentheses by solving the multiplications.

`\begin{gathered} (5\cdot9x+5\cdot(-1)+6\cdot2x+6\cdot(-10))/(30) \\ (45x-5+12x-60)/(30) \end{gathered}`

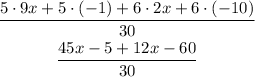
Adding like terms:

`\begin{gathered} (45x+12x-5-60)/(30) \\ (57x-65)/(30) \end{gathered}`

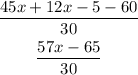
Answer:

`(57x-65)/(30)`