We want to solve the following equations:
item (a):
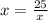
To solve this one, let's start by multiplying both sides by x.
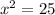
Now, let's take the square root of both sides
![\begin{gathered} \sqrt[]{x^2}=\sqrt[]{25} \\ x=\pm5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y49hmt699o26wjlrbno0ddnl129dsxj58f.png)
The solutions for this equation are x = 5 and x = -5.
item (b):
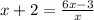
To solve this one, let's again start by multiplying both sides by x.
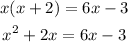
Now, let's subtract 2x from both sides.
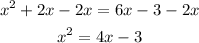
Let's rewrite this equation with all terms in the right side
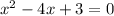
Factorizing

Since this is a product of two terms, the result will be zero only if one of them is zero.
Then, we get two equations
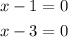
The solutions for those two equations are the solutions for our system.
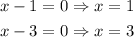
The solutions for this equation are x = 1 and x = 3.
item (c):
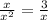
Let's start by solving the division in the right side
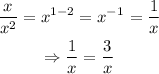
Multiplying both sides by x, we have:
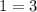
Since this statement is false, this equation have no solution.
item (d):
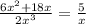
Let's start by multiplying both sides by x.
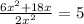
Doing the division on the left side of the equality, we have:
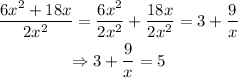
Subtracting 3 from both sides:
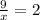
Multiplying both sides by x again:
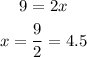
The solution for this system is x = 4.5.