Question

the datafor each grade have the same interquartile range. which of the following best compares the twotest score distribution?

Answer 1

We are given the dot-plots of sixth-grade test scores and seventh-grade test scores.

Let us first find the median of the two test scores.

Recall that the median is the value that divides the distribution into two equal halves.

Sixth Grade Geograph Test Scores:

From the dot-plot, we see that 11 is the median test score since it divides the distribution into two equal halves.

Median = 11

Seventh Grade Geograph Test Scores:

From the dot-plot we see that 13 is the median test score since it divides the distribution into two equal halves.

Median = 13

Therefore, the median score of the seventh-grade class is 2 points greater than the median score of the sixth-grade class.

Now let us find the interquartile range which is given by

`IQR=Upper\: quartile-Lower\: quartile`

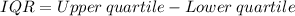
Seventh Grade Geograph Test Scores:

The upper quartile is given by

At the 10th position, we have a test score of 13

The lower quartile is given by

At the 3rd position, we have a test score of 11

So, the interquartile range is

`IQR=Upper\: quartile-Lower\: quartile=13-11=2`

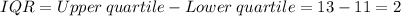
Sixth Grade Geograph Test Scores

The upper quartile is given by

At the 9th position, we have a test score of 10

The lower quartile is given by

At the 3rd position, we have a test score of 8

So, the interquartile range is

`IQR=Upper\: quartile-Lower\: quartile=10-8=2`

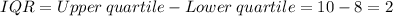
So, the IQR is the same as the difference between medians.

Therefore, the median score of the seventh-grade class is 2 points greater than the median score of the sixth-grade class. The difference is the same as the IQR

Hence, the correct answer is option B