Step-by-step explanation
From the statement, we know that the silo has two parts:
• the top is a hemisphere with a radius r = 5 ft,
,
• the body is a right circular cylinder with a radius r = 5ft, and height h,
,
• the total capacity of the silo is a volume Vₜ = 614 π ft³.
The total volume of the silo Vₜ is given by the sum of the volume of each part:
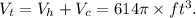
Where Vₕ is the volume of the hemisphere and Vc is the volume of the cylinder.
(1) The volume of the hemisphere is given by:
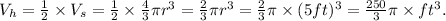
(2) The volume of the cylinder is given by:
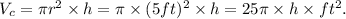
(3) Replacing the results from points (1) and (2) in the equation of the total volume, we have:
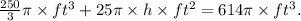
Solving for h, we get:
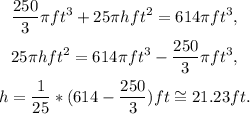
Answer
The height of the silo is 21.23 ft to the nearest hundredth of a ft.