Question

a grain silo has the shape of a right circular cylinder topped by a hemisphere. If the silo is to have a capacity of 614 π cubic feet, find the height of a silo with a radios 5 feet. round to the nearest hundredth of a foot

Answer 1

Step-by-step explanation

From the statement, we know that the silo has two parts:

• the top is a hemisphere with a radius r = 5 ft,

,

• the body is a right circular cylinder with a radius r = 5ft, and height h,

,

• the total capacity of the silo is a volume Vₜ = 614 π ft³.

The total volume of the silo Vₜ is given by the sum of the volume of each part:

`V_t=V_h+V_c=614\pi* ft^3.`

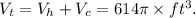
Where Vₕ is the volume of the hemisphere and Vc is the volume of the cylinder.

(1) The volume of the hemisphere is given by:

`V_h=(1)/(2)* V_s=(1)/(2)*(4)/(3)\pi r^3=(2)/(3)\pi r^3=(2)/(3)\pi*(5ft)^3=(250)/(3)\pi* ft^3.`

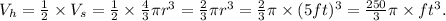
(2) The volume of the cylinder is given by:

`V_c=\pi r^2* h=\pi*(5ft)^2* h=25\pi* h* ft^2.`

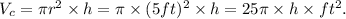
(3) Replacing the results from points (1) and (2) in the equation of the total volume, we have:

`(250)/(3)\pi* ft^3+25\pi* h* ft^2=614\pi* ft^3.`

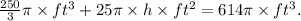
Solving for h, we get:

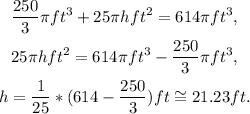
`\begin{gathered} (250)/(3)\pi ft^3+25\pi hft^2=614\pi ft^3, \\ 25\pi hft^2=614\pi ft^3-(250)/(3)\pi ft^3, \\ h=(1)/(25)*(614-(250)/(3))ft\cong21.23ft. \end{gathered}`Answer

The height of the silo is 21.23 ft to the nearest hundredth of a ft.