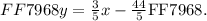Question

8,-4);3x-5y=8 slope parallel ?

Answer 1

Let us first bring the equation given into the slope-intercept form.

`\begin{gathered} 3x-5y=8, \\ 5y=3x-8, \\ \rightarrow\textcolor{#FF7968}{y=(3)/(5)x-(8)/(5).} \end{gathered}`

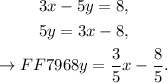
We see that the above equation has slope 3/ 5, and therefore, the equation that we want to construct must also have this slope. Hence, we already know that the equation we are seeking must take the form

`y=(3)/(5)x+b`

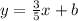
where b is the y-intercept yet unknown.

Let us plug in (x, y) = (8, -4) in the above equation, this gives

`-4=(3)/(5)(8)+b`
`-4=(24)/(5)+b`
`\therefore b=-(44)/(5)\text{.}`

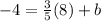
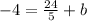
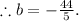
Hence, the equation of the line in slope-intercept form is

`\textcolor{#FF7968}{y=(3)/(5)x-(44)/(5)}\text{\textcolor{#FF7968}{.}}`