Let us first bring the equation given into the slope-intercept form.
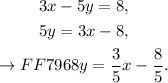
We see that the above equation has slope 3/ 5, and therefore, the equation that we want to construct must also have this slope. Hence, we already know that the equation we are seeking must take the form
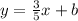
where b is the y-intercept yet unknown.
Let us plug in (x, y) = (8, -4) in the above equation, this gives

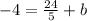
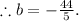
Hence, the equation of the line in slope-intercept form is
