Question

N zo 113° M P In the figure above, MNO is an isosceles triangle with MN = NP. What NP. What is the value of x ?

Answer 1

We have an isosceles triangle.

As MN and PN are the sides that are equal to each other, the angles M and P have the same measure.

We can find the measure of P as it is the supplementary to 113 degrees.

We then can write:

`\begin{gathered} m\angle P+113=180 \\ m\angle P=180-113 \\ m\angle P=67 \end{gathered}`

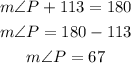
As mP and mM are equal to 67 degrees, and the sum of the measures of the internal angles of a triangle is equal to 180 degrees, we can write:

`\begin{gathered} m\angle P+m\angle M+m\angle N=180 \\ m\angle N=180-(m\angle P+m\angle M) \\ m\angle N=180-(67+67) \\ m\angle N=180-134 \\ m\angle N=46 \end{gathered}`

Now, to find x, we use the information that the angle x and Nare complementary. That means that their measures add 90 degrees.

So we can write:

`\begin{gathered} m\angle N+x=90 \\ 46+x=90 \\ x=90-46 \\ x=44\degree \end{gathered}`

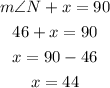
Answer: x = 44 degrees.