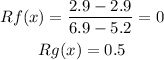Question

Consider the graphs of f(x) and g(x) below:For each interval given below, calculate the average rate of change of f(x) or g(x) and compare the results.i. [0, 4]ii. [0, 8]iii. [0, 2.2]iv. [5.2, 6.1]v. [5.2, 6.9]

Answer 1

`\begin{gathered} 1)\text{ Rf(x)=0 Rg(x)=0.5} \\ 2.\text{ Rf(x)=0 Rg(X)=0.5} \\ 3)\text{ Rf(x)=1.32 Rg(x)=0.5} \\ 4)\text{ Rf(x)=2.22 Rg(x)=0.5} \\ 5)\text{ Rf(x)=0 Rg(x)=0.5} \end{gathered}`

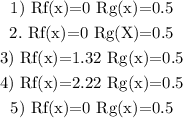
Explanation:

To determine the average rate of change of an interval [a,b], we must use the following equation:

`(f(b)-f(a))/(b-a)`

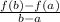
Therefore, for the interval [0,4]:

`ratef(x)=(0-0)/(4-0)=0`

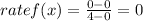
For g(x) we need to find the equation of the line by the slope-point form:

`\begin{gathered} y-y_0=m(x-x_0) \\ y-2.9=((4.9-2.9)/(6.1-2.2))(x-2.2) \\ y-2.9=(20)/(39)(x-2.2) \\ y=(20)/(39)x-(44)/(39)+2.9 \\ y=(20)/(39)x+(691)/(390) \end{gathered}`

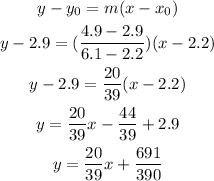
To find the value to x=4, substitute it into the equation:

`\begin{gathered} y=(20)/(39)(4)+(691)/(390) \\ y=3.82 \\ \text{ Rate of change:} \\ \text{ Rate g(x)=}(3.8-1.77)/(4-0)=0.5 \end{gathered}`

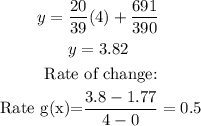
Now, for [0,8]:

`\begin{gathered} Rf(x)=(0-0)/(8-0)=0 \\ Rg(x)=(5.87-1.77)/(8-0)=0.5 \end{gathered}`

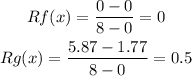
[0,2.2]:

Since g(x) is a linear function, it will have a constant rate of change 0.5.

f(x):

`Rf(x)=(2.9-0)/(2.2-0)=1.32`

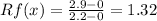
[5.2, 6.1]:

`\begin{gathered} Rf(x)=(4.9-2.9)/(6.1-5.2)=2.22 \\ Rg(x)=0.5 \end{gathered}`

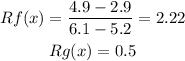
[5.2,6.9]:

`\begin{gathered} Rf(x)=(2.9-2.9)/(6.9-5.2)=0 \\ Rg(x)=0.5 \end{gathered}`