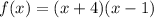
To find the zeros of the function we equal the function to 0
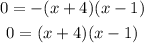
since this is a product, it can be 0 when one of the factors is equal to zero, for that reason:
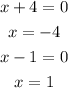
the zeros of the function are x=-4 and x=1.
after that to do the sketch find the vertex which can be found by
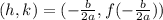
according to the function a=-1, b=-3 and c=4
the vertex is
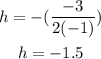
using the function find k
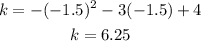
the vertex is at (-1.5,6.25)
the graph should look like this