Question

The graph of f' (x), the derivative of f(x), is continuous for all x and consists of five line segments as shown below. Given f (5) = 10, find the absolute minimum value of f(×) over the interval [0, 5].

Answer 1

Looking at the graph

we have that

For the interval (-3,0) the slope is negative ---> function f(x) is decreasing

For the interval (0,2) the slope of the first derivative is positive ---> the function f(x) is increasing

so

at x=0 there is a minimum value

The equation of the derivative at the interval (-3,0) is y'=-x

The equation of the derivative at the interval (0,2) is y'=x

The equation of the derivative at the interval (2,4) is y'=2x

The equation of the derivative at the interval (4,5) is

we have the points

(4,2) and (5,0)

Find out the slope

m=(0-2)/(5-4)

m=-2/1

m=-2

Find out the equation of the line

y=mx+b

m=-2

point (5,0)

substitute and solve for b

0=-2(5)+b

b=10

therefore

y'=-2x+10

Find out the function f(x) at the interval (4,5)

`f(x)=\int_^(-2x+10)dx=-x^2+10x+c`

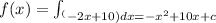
Remember that

f(5)=10

Find out the value of C

For x=5

-(5)^2+10(5)+C=10

-25+50+C=10

C=-15

therefore

f(x)=-x^2+10x-15 -------------> interval (4,5)

For x=4 ------> f(x)=-(4)^2+10(4)-15=-16+40-15=9

Part 2

Find out the equation of the function f(x) at the interval (2,4)

y'=2 -------> applying the integral ------> f(x)=2x+C

Remember that

For x=4 ----> f(x)=9

Find out the value of C

9=2(4)+C

C=1

therefore

f(x)=2x+1 -------------> interval (2,4)

For x=2 -----> f(x)=2(2)+1=5

Part 3

Find out the equation of f(x) at the interval (0,2)

y'=x ----> applying the integral -----> f(x)=(1/2)x^2+C

Remember that

For x=2 ---> f(x)=5

5=(1/2)(2)^2+C

5=2+C

C=3

therefore

f(x)=(1/2)x^2+3 ------> interval (0,2)

For x=0 ---------> f(x)=3

Part 4

Find out the equation of f(x) at the interval (-3,0)

y'=-x ------> f(x)=-(1/2)x^2+C

For x=0 ------> f(x)=3

so

3=-(1/2)(0)^2+C

C=3

therefore

f(x)=-(1/2)x^2+3 ------> interval (-3,0)

Part 5

Graph the given functions

The absolute minimum value is f(x)=3 at x=0