Use the substitution method to solve the system of equations.
Let k be the cost of a knife and s be the cost of a spoon.
Since a knife is four times the cost of a spoon, then:
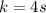
Since 12 spoons and 16 knives cost 105.64, then:
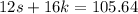
Replace the expression for k in terms of s into the second equation:
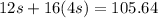
We obtained an equation in a single variable. Solve for s:
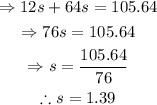
Replace the value of s into the expression for k to find the cost of a knife:
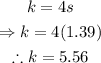
Therefore, the cost of one knife is equal to £5.56.