The given polynomial function is;
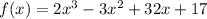
Firstly, we would find a factor of the function by a trial and error method.
Thus, we have:

We are going to use the long division method to get the other factor(s).
Thus, we have:
The final remainder of the long division is 0.
Thus, the factors of the polynomial are:
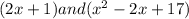
Find the zeros of these factors, we have:
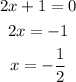
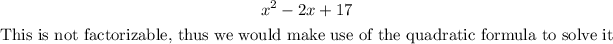
The quadratic formula is given by the equation;
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
![\begin{gathered} \text{From the equation;} \\ x^2-2x+17 \\ a=1;b=-2;c=17 \\ \text{Thus, we have} \\ x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4(1)(17)}}{2(1)} \\ x=\frac{2\pm\sqrt[]{4-68}}{2} \\ x=\frac{2\pm\sqrt[]{-64}}{2} \\ \text{Recall from complex number;} \\ i=\sqrt[]{-1} \\ \text{Thus, }\sqrt[]{-64}\text{ can be further expressed as }\sqrt[]{64}\text{ }*\sqrt[]{-1} \\ \Rightarrow8i \\ \text{Thus, } \\ x=(2\pm8i)/(2) \\ x=(2+8i)/(2)\text{ OR }(2-8i)/(2) \\ x=(2(1+4i))/(2)\text{ OR }(2(1-4i))/(2) \\ x=1+4i_{} \\ OR \\ x=1-4i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/iri83y36h3swx317tfvot9u0jo78qi806r.png)
Hence, the solutions are:
