Question

the difference quotient for this problem. i don’t understand the steps to take to apply the formula of f(x+h)-f(x) /h

Answer 1

The formula of x+h to find the difference quotient is:

`(f(x+h)-f(x))/(h)`

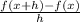
Then, in this case we want to know what happens near 7, we add an infinitely smal portion called h.

Then to find the diference quotient at x near 7:

`\frac{\sqrt[]{7(7+h)}-\sqrt[]{7\cdot7}}{h}`

Then we can solve the root and the parentheses:

`\frac{\sqrt[]{49+7h}-7}{h}`

Now we can multiply by the conjugate:

`\frac{\sqrt[]{49+7h}-7}{h}\cdot\frac{\sqrt[]{49+7h}+7}{\sqrt[]{49+7h}+7}=\frac{(\sqrt[]{49+7h})^2-7\sqrt[]{49+7h}+7\sqrt[]{49+7h}-49}{h(49\sqrt[]{49+7h})}`

Then there is two terms in the top we can cancel out, and is often easier if we dont distribute the product on the denominator.

Next:

`\frac{49+7h-49}{h(49\sqrt[]{49+7h})}`

We have just:

`\frac{7h}{h(49\sqrt[]{49+7h})}`

Then we can cancel out:

`\frac{7}{49\sqrt[]{49+7h}}`