Question

Please help with this question all parts check part A And answer b - e

Answer 1

Given:

Xavier set contains one blue ink refill and one black ink refill.

Yvonne set contains two blue ink refill, three black ink refill and one red ink refill.

Zena set contains four blue ink refill, five black ink refill and one red ink refill.

To find:

(A) Representation of variables:

(B) The system of linear equation:

(C) Solving the equation using gauss Jordan elimination:

Step-by-step solution:

(A) Representation of variables:

X = Number of Xavier set to sell

Y = Number of Yvonne set to sell

Z = Number of Zena set to sell

B) The system of linear equation:

x + 2y + 4z = 11

x + 3y + 5z = 14

y + z = 3

C) Solving the equation using gauss Jordan elimination:

`\begin{gathered} \begin{bmatrix}{1} & 2 & {4} \\ {1} & {3} & {5} \\ {0} & {1} & {1}\end{bmatrix}\begin{bmatrix}{} & {11} & {} \\ {} & {14} & {} \\ {} & {3} & {}\end{bmatrix} \\ R_2=R_2-R_1 \\ \begin{bmatrix}{1} & {2} & {4} \\ {0} & {1} & {1} \\ {0} & {1} & {1}\end{bmatrix}\begin{bmatrix}{} & {11} & {} \\ {} & {3} & {} \\ {} & {3} & {}\end{bmatrix} \\ R_1=R_1-2R_2 \\ R_3=R_3-R_1 \\ \begin{bmatrix}{1} & {0} & {2} \\ {0} & {1} & {1} \\ {0} & {1} & {1}\end{bmatrix}\begin{bmatrix}{} & {5} & {} \\ {} & {3} & {} \\ {} & {0} & {}\end{bmatrix} \\ \end{gathered}`

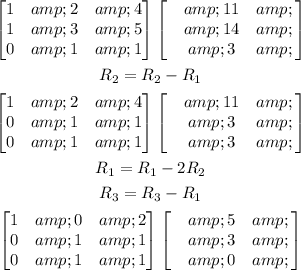
From here we can say that:

x + 2z = 5

y + z = 3

z = free variable

Let z = 2

x + 4 = 5

x = 1

y + 2 = 3

y = 1

Thus the triplet is (1,1,2)

Also,

x = 0, y = 0.5 and z = 2.5

or

x = 1, y = 1 and z = 2

D) Possible combination all sets company can offer:

x = 0, y = 0.5 and z = 2.5

x = 1, y = 1 and z = 2

We can directly use them as sets.

E) Solution in terms of variables represent:

The link company needs to sell 1 Xavier set, 1 Yvonne set and 2 Zena set.