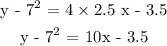ANSWER
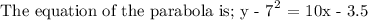
EXPLANATION
Given that;
The focus of the parabola is (6, 7)
The directrix is 1
Follow the steps below to find the equation of the parabola
Step 1; Write the general formula of the parabola equation
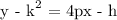
Recall, that the vertex of the parabola midway between the focus and directrix
Hence, h can be calculated below has
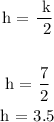
Also, p is the distance of vertex to directrix
p = 6 - 3.5
p = 2.5
Step 2; Substitute the calculated data into the formula in step 1