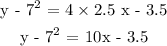Question

Write the equation for a parabola with a focus at (6, 7) and a directrix at x = 1.

Answer 1

x=(y-7)^2/10 +7/2

Explanation:

khan

Answer 2

`\text{ The equation of the parabola is; \lparen y - 7\rparen}^2\text{ = 10\lparen x - 3.5\rparen}`

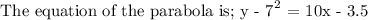
EXPLANATION

Given that;

The focus of the parabola is (6, 7)

The directrix is 1

Follow the steps below to find the equation of the parabola

Step 1; Write the general formula of the parabola equation

`\text{ \lparen y - k\rparen}^2\text{ = 4p\lparen x - h\rparen}^`

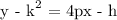
Recall, that the vertex of the parabola midway between the focus and directrix

Hence, h can be calculated below has

`\begin{gathered} \text{ h = }\frac{\text{ k}}{\text{ 2}} \\ \\ \text{ h = }(7)/(2) \\ \text{ h = 3.5} \end{gathered}`

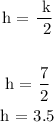
Also, p is the distance of vertex to directrix

p = 6 - 3.5

p = 2.5

Step 2; Substitute the calculated data into the formula in step 1

`\begin{gathered} \text{ \lparen y - 7\rparen}^2\text{ = 4}*2.5\text{ \lparen x - 3.5\rparen} \\ \text{ \lparen y - 7\rparen}^2\text{ = 10\lparen x - 3.5\rparen} \end{gathered}`