Given the function
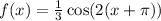
Which is equivalent to
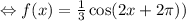
In general, a trigonometric equation has the following structure
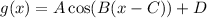
Where A is the amplitude.
Therefore, the amplitude of our function is 1/3.
As for the minimum and maximum of the function, remember that the range of the cosine function is [-1,1]; therefore,
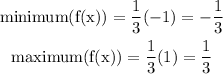
Furthermore, the midline of the graph is a parallel line to the x-axis that crosses the midpoint between the maximum and the minimum; in our case,

Finally, the graph of the function in the [0,2pi] interval is