Question

In a solid hemisphere, a cone with radius 4 inches and height 4 inches is removed as shown. Calculate the volume of the shaded region.

Answer 1

In the given figure, we have a hemisphere and inside it we have a cone.

Recall that the volume of a hemisphere is given by

`V_h=(2)/(3)\pi r^3`

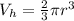
Where r is the radius of the hemisphere.

For the given case, the radius is 4 inches

`V_h=(2)/(3)\pi(4)^3=(2)/(3)\pi(64)=(128\pi)/(3)\: in^3`

So, the volume of the hemisphere is 128π/3 cubic inches.

Recall that the volume of a cone is given by

`V_c=(1)/(3)\pi r^2h`

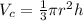
Where r is the radius and h is the height of the cone.

For the given case, the radius is 4 inches and the height is 4 inches

`V_c=(1)/(3)\pi(4)^2(4)=(1)/(3)\pi(16)^{}(4)=(64\pi)/(3)\: in^3`

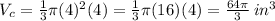
So, the volume of the cone is 64π/3 cubic inches.

Finally, notice that if you subtract the volume of the cone from the volume of the hemisphere then what is left is the volume of the shaded region.

So, the volume of the shaded region is

`\begin{gathered} V_S=V_h-V_c \\ V_S=(128\pi)/(3)-(64\pi)/(3) \\ V_S=(64\pi)/(3) \\ V_S=67.0\: in^3 \end{gathered}`

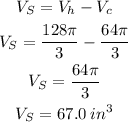
Therefore, the volume of the shaded region is 67.0 cubic inches.