Question

I’m not sure if I was doing this correctly and I am a bit confused. This wheel has a radius of 32 feet and a distance from the center to the Ferris wheel to the ground is 40! The ferris wheel spin clockwise and the rider is located at booth A.

Answer 1

We have a total of 12 booths equally distributed through the Ferris Wheel. If the rider is located at booth A, to get to the highest point of the Ferris Wheel he needs to travel 9 "positions" until he gets there. Since the wheel takes 16 minutes to do a complete rotation, the amount of time it will take for the rider to get to the highest point will be given by

`(9)/(12)\cdot16=12`

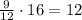
It will take 12 minutes.

To get from the position of one booth to the next one, we just need to divide the total amount of time it takes to do a complete rotation by the amount of booths.

`(16)/(12)=(4)/(3)`

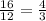
This is the time needed to get from one position to the next one. Between the booths A and K, the booth moves 2 "positions", therefore the time it will take for him to move from A to K is

`2\cdot(4)/(3)=(8)/(3)=2(2)/(3)\approx2.66`

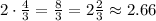
It will take 2.66 minutes to get from position A to position K.