Question

If Tobias has 2 times as many quarters as nickels and they have a combined value of 275 cents, how many of each coin does he have?

Answer 1

Given:

Tobias has 2 times as many quarters as nickels.

They have a combined value of 275 cents.

To find:

The number of each coin.

Step-by-step explanation:

Let q be the number of quarters.

Let n be the number of nickels.

Since he has 2 times as many quarters as nickels.

`q=2n.........(1)`

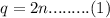
We know that,

`\begin{gathered} 1\text{ }quarter=25\text{ }cents \\ 1\text{ }nickel=5\text{ }cents \end{gathered}`

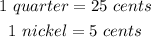
According to the problem,

`25q+5n=275........(2)`

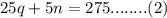
Substituting equation (1) in (2), we get

`\begin{gathered} 25(2n)+5n=275 \\ 50n+5n=275 \\ 55n=275 \\ n=(275)/(55) \\ n=5 \end{gathered}`

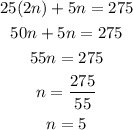
From (1), we get

`q=2n=2(5)=10`

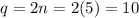
Therefore, the number of quarters is 10 and the number of nickels is 5.

Final answer:

• The number of quarters is 10.

,

• The number of nickels is 5.