Answer:
![\textbf{A}^(-1) =\left[ \begin{array}{cc}-30&71\\-11&26\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/qx9i1xqkx38qoiz1ldf1x8l9aiitimlh59.png)
![\textbf{X}=\left[\begin{array}{c}-4\\7\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/7yblhyz1xlo7dxcw8zr05z1csiio37heqt.png)
Explanation:
The inverse of a matrix M is the matrix M⁻¹.
![\textsf{If}\; \textbf{M} = \left[ \begin{array}{cc}a&b\\c&d\end{array}\right] \; \textsf{then} \; \textbf{M}^(-1)=\frac{1}{\text{det} \;\textbf{M}}\left[ \begin{array}{cc}d&-b\\-c&a\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/q1tdeb6qlxlqi2xhdvmxt12xhn8v1nww2d.png)
![\textsf{For a $2 * 2$ matrix} \; \textbf{M}=\left[\begin{array}{cc}a&b\\c&d\end{array}\right], \; \textsf{the determinant of} \; \textbf{M} \; \textsf{is $ad-bc$}.](https://img.qammunity.org/2023/formulas/mathematics/high-school/j5cdhdexmip52396nz3lwrxie58v1x30d7.png)
Given matrix:
![\textbf{A}=\left[\begin{array}{cc}26&-71\\11&-30\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/tm69mbvqs56a2mmsxgs0vzjqxkjrql1cqq.png)
Therefore:
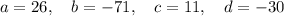
Calculate the determinant of matrix A:
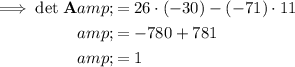
Therefore, the inverse of matrix A is:
![\begin{aligned}\implies \textbf{A}^(-1) & =(1)/(1)\left[ \begin{array}{cc}-30&71\\-11&26\end{array}\right]\\\\&=\left[ \begin{array}{cc}-30&71\\-11&26\end{array}\right]\end{aligned}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ovoo2kf07uioqzkqdg0hgewyt5pbhtz4w5.png)
------------------------------------------------------------------------------------------
Given matrices:
![\textbf{A}=\left[\begin{array}{cc}26&-71\\11&-30\end{array}\right], \quad \textbf{B}=\left[\begin{array}{c}-49\\-132\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/6lo7qhnm0dgw5n9nu8ktumi30rmxr75s4t.png)
![\textsf{Let}\;\textbf{X}=\left[\begin{array}{c}p\\q\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/ifacmy1xkfaka5znjb7fqlv0jie1jxb4hx.png)
If AX = B then:
![\implies\left[\begin{array}{cc}26&-71\\11&-30\end{array}\right]\left[\begin{array}{c}p\\q\end{array}\right]=\left[\begin{array}{c}-49\\-132\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/6pc4uhpxon49h66rbov5d9dwgxoq2vldkt.png)
![\implies\left[\begin{array}{c}7p+(-3)q\\19p+(-8)q\end{array}\right]=\left[\begin{array}{c}-49\\-132\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/v2tc68eyqohr96o4arec3z65ltu94epbem.png)
Therefore:
Solving simultaneously:
Therefore:
![\implies \textbf{X}=\left[\begin{array}{c}-4\\7\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/a6ckyxjv3itj62lzhb8i6edx38egq33taa.png)