Answer: False
=========================================================
Step-by-step explanation:
If you prefer the pythagorean theorem, then follow the method mentioned by the other response.
I'll use the distance formula as a slight alternative. In fact, the distance formula is a modified version of the pythagorean theorem.
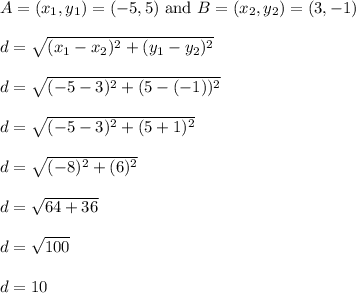
The result of the distance formula calculation shows the distance from A(-5,5) to B(3,-1) is exactly 10 units.
This means segment AB is exactly 10 units long.
Therefore, the statement "the line segment is 36 units long" is false