Question

Consider the following word problem:A pizzeria sells three sizes of pizza: small, medium, and large. The pizzas sell for S7, S10, and SII.respectively. One evening they sold 47 pizzas and received $469. If they sold 17 more large than smallpizzas, how many of each size did they sell?Use the Gaussian elimination method with back substitution to solve the given word problem.AnswerHow to enter your answer (opens in new window)KeypadKeyboard Shortcutssmall=medium=large=

Answer 1

System of Equations

Let:

x = number of small pizzas

y = number of medium pizzas

z = number of large pizzas

They sold 47 pizzas, thus:

x + y + z = 47

They received 7x for the small pizzas, 10y for the medium pizzas, and 11z for the large pizzas, thus:

7x + 10y + 11z = 469

The last condition states they sold 17 more large than small pizzas, thus:

z = 17 + x

Rearranging the system of equations:

x + y + z = 47

7x + 10y + 11z = 469

x + 0y - z = -17

Now we write the expanded matrix of the system:

`\begin{bmatrix}1{} & {1} & {1} & {47} \\ {7} & {10} & {11} & {469} \\ {1} & {0} & {-1} & {-17} \\ {} & {} & {} & {}\end{bmatrix}`

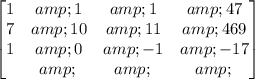
Apply Gauss-Jordan Elimination Method.

Multiply row 1 by -7 and add it to row 2:

`\begin{bmatrix}1{} & {1} & {1} & {47} \\ 0 & 3 & 4 & 140 \\ {1} & {0} & {-1} & {-17} \\ {} & {} & {} & {}\end{bmatrix}`

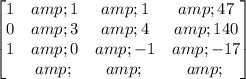
Divide row 2 by 3:

`\begin{bmatrix}1{} & {1} & {1} & {47} \\ 0 & 1 & (4)/(3) & (140)/(3) \\ {1} & {0} & {-1} & {-17} \\ {} & {} & {} & {}\end{bmatrix}`

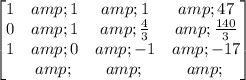
Multiply row 2 by -1 and add it to row 1:

`\begin{bmatrix}1{} & 0 & -(1)/(3) & (1)/(3) \\ 0 & 1 & (4)/(3) & (140)/(3) \\ {1} & {0} & {-1} & {-17} \\ {} & {} & {} & {}\end{bmatrix}`

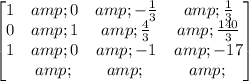
Multiply row 1 by -1 and add it to row 3:

`\begin{bmatrix}1{} & 0 & -(1)/(3) & (1)/(3) \\ 0 & 1 & (4)/(3) & (140)/(3) \\ 0 & {0} & -(2)/(3) & {-(52)/(3)} \\ {} & {} & {} & {}\end{bmatrix}`

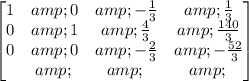
Multiply row 3 by -3/2:

`\begin{bmatrix}1{} & 0 & -(1)/(3) & (1)/(3) \\ 0 & 1 & (4)/(3) & (140)/(3) \\ 0 & {0} & 1 & 26 \\ {} & {} & {} & {}\end{bmatrix}`

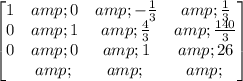
Multiply row 3 by 1/3 and add it to row 1:

`\begin{bmatrix}1{} & 0 & 0 & 9 \\ 0 & 1 & (4)/(3) & (140)/(3) \\ 0 & {0} & 1 & 26 \\ {} & {} & {} & {}\end{bmatrix}`

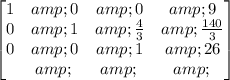
Multiply row 3 by -4/3 and add it to row 2:

`\begin{bmatrix}1{} & 0 & 0 & 9 \\ 0 & 1 & 0 & 12 \\ 0 & {0} & 1 & 26 \\ {} & {} & {} & {}\end{bmatrix}`

Now we have the identity matrix 3x3 to the left and the column of solutions to the right:

x = 9, y = 12, z = 26

They sold 9 small pizzas, 12 medium pizzas, and 26 large pizzas