System of Equations
Let:
x = number of small pizzas
y = number of medium pizzas
z = number of large pizzas
They sold 47 pizzas, thus:
x + y + z = 47
They received 7x for the small pizzas, 10y for the medium pizzas, and 11z for the large pizzas, thus:
7x + 10y + 11z = 469
The last condition states they sold 17 more large than small pizzas, thus:
z = 17 + x
Rearranging the system of equations:
x + y + z = 47
7x + 10y + 11z = 469
x + 0y - z = -17
Now we write the expanded matrix of the system:
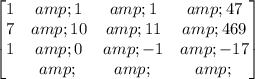
Apply Gauss-Jordan Elimination Method.
Multiply row 1 by -7 and add it to row 2:
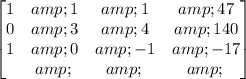
Divide row 2 by 3:
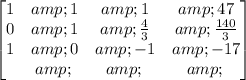
Multiply row 2 by -1 and add it to row 1:
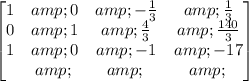
Multiply row 1 by -1 and add it to row 3:
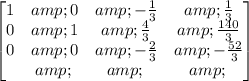
Multiply row 3 by -3/2:
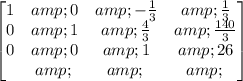
Multiply row 3 by 1/3 and add it to row 1:
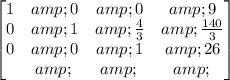
Multiply row 3 by -4/3 and add it to row 2:

Now we have the identity matrix 3x3 to the left and the column of solutions to the right:
x = 9, y = 12, z = 26
They sold 9 small pizzas, 12 medium pizzas, and 26 large pizzas