We want to find the measure of the ∠ACE. For doing so, we are going to use some geometrical properties with the information given.
As D is the midpoint of AB, we have that:

And as E is the midpoint of BC, we have:

Moreso, we can say that:
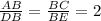
And thus, the sides are proportional. As both triangles have the angle:
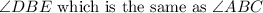
We can say that the triangles ABC and DBE are similar by the Theorem SAS (side-angle-side):
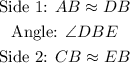
Thus, their sides are proportional, and their corresponding angles are congruent.
As the angles ACE and DEB are corresponding (on the two triangles), they have the same measure:
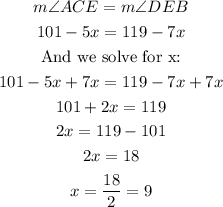
This means that the value of x is 9. Now, replacing on the value of ACE, and we get:
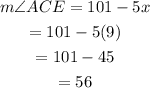
Thus, the value of the angle ∠ACE is 56°.