STEP 1: We are to factor the quadratic
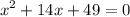
This will result in two linear factors;
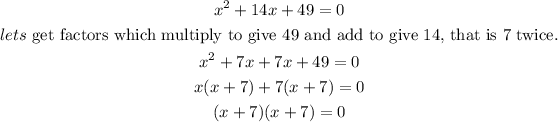
Thus, the factored form is ( x + 7)( x + 7)=0
STEP 2: We are to solve the equation by factoring,
we have already factored the equation as;
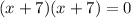
For this to be true (x + 7) has to be equal to zero, i.e
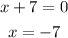
Therefore x = - 7 (twice)