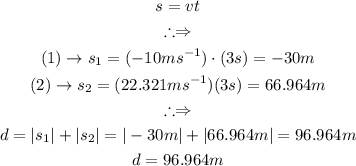Answer:
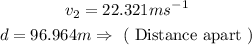
Step-by-step explanation: This problem can be solved using the conservation of momentum concept, the equations used are as follows:

The knowns and unknowns in equation (1) and (2) are as follows:
![\begin{gathered} m_1=87.5\operatorname{kg} \\ v_1=-10ms^(-1) \\ m_2=39.2\operatorname{kg} \\ v_2=\text{?} \\ v_i=0 \end{gathered}]()
Plugging these values in (1) and (2) gives us the following result:
![\begin{gathered} (1)=(2) \\ \therefore\Rightarrow \\ (m_1+m_2)(0)=m_1v_1+m_2v_2=0 \\ (87.5\operatorname{kg})(-10ms^(-1))+(39.2\operatorname{kg})v_2=0 \\ v_2=\frac{(87.5\operatorname{kg})(10ms^(-1))}{(39.2\operatorname{kg})}=22.321ms^(-1) \\ v_2=22.321ms^(-1) \end{gathered}]()
To calculate the distance travelled in 3 seconds, we simply do as follows: