Question

2.The number of grams A of a certain radioactive substance present at time, in yearsfrom the present, t is given by the formulaA = 45e^-0.0045ta. What is initial amount of this substance?b. What is half-life of this substance?c. How much will be around in 2500 years?

Answer 1

Given that,

The number of grams A of a certain radioactive substance present at time, in years

from the present, t is given by the formula

`A=45e^(-0.0045(t))`

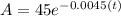
a) To find the initial amount of this substance

At t=0, we get

`A=45e^(-0.0045(0))`
`A=45e^0`

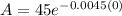
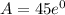
We know that e^0=1 ( anything to the power zero is 1)

we get,

`A=45`

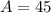
The initial amount of the substance is 45 grams

b)To find thehalf-life of this substance

To find t when the substance becames half the amount.

A=45/2

Substitute this we get,

`(45)/(2)=45e^(-0.0045(t))`

`(1)/(2)=e^(-0.0045(t))`

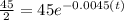
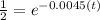
Taking natural logarithm on both sides we get,

`\ln ((1)/(2))=-0.0045(t)^{}`
`(-1)\ln ((1)/(2))=0.0045(t)`
`\ln ((1)/(2))^(-1)=0.0045(t)`
`\ln (2)=0.0045(t)`
`0.6931=0.0045(t)`
`t=(0.6931)/(0.0045)`
`t=154.02`

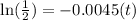
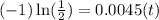
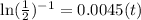
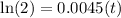
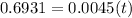
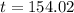
Half-life of this substance is 154.02

c) To find the amount of substance will be present around in 2500 years

Put t=2500

we get,

`A=45e^(-0.0045(2500))`
`A=45e^(-11.25)`
`A=45*0.000013=0.000585`
`A=0.000585`

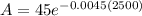
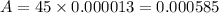
The amount of substance will be present around in 2500 years is 0.000585 grams