Answer:
account 1 investment: 18,000
account 2 investment: 8,500
Step-by-step explanation:
Let us call A0 and B0 the principle amount in each account, then we know that
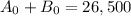
Furthermore, the simple interest earned on account A0, for example, is
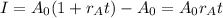
where A0 ( 1+ rt) is the account balance after time t on simple interest. If we subtract the initial balance from the final, we would get the total interest earned. The expression above finds exactly just that ( the interest earned).
Now the interest earned on account B0 is
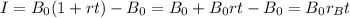
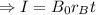
Now we know that the total interest earned is $1970, therefore,
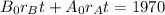
putting in rA = 10% = 0.10 , rB = 2% = 0.02, and t = 1 gives us the system:
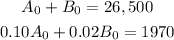
Now, this is a system of equations with unknowns A0 and B0.
We multiply the first equation by 0.10 t0 get:
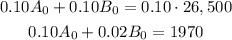
subtracting the second equation from the first gives
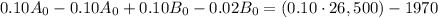
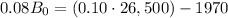
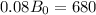
finally, dividing both sides by 0.08 gives
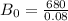
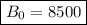
which is our answer!
Now that we have the value of B0, we now find the value of A0 from the following equation:
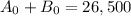
putting in b0 = 8500 gives
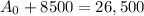
finally, subtracting 8500 from both sides gives
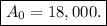
which is our answer!
Hence, the amount invested in the accounts was 8,500 and 18,000.