Question

Solve the system by substitution.5x - 2y + 3z = 6-2x - 4y - 3z = 142 + 6y - 8z = 12yPls see the picture

Answer 1

Given the System of Equations:

`\begin{cases}5x-2y+3z=6 \\ \\ 2x-4y-3z=14 \\ \\ x+6y-8z=12\end{cases}`

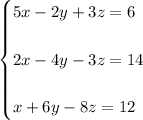
You can solve it using the Substitution Method:

1. Solve for "y" from the third equation:

`\begin{gathered} 6y=12-x+8z \\ \\ y=2-(x)/(6)+(4z)/(3)\text{ (Equation I)} \end{gathered}`

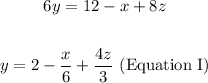
2. Add the first and the second equation:

`\begin{gathered} \begin{cases}5x-2y+3z=6 \\ \\ 2x-4y-3z=14 \\ \end{cases} \\ ---------------- \\ 7x-6y=20\text{ (Equation II)} \end{gathered}`

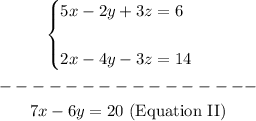
3. Solve for "y" from Equation I:

`\begin{gathered} -6y=20-7x \\ \\ y=(20)/(-6)-(7)/((-6))x \\ \\ y=-(10)/(3)+(7)/(6)x\text{ (Equation III)} \end{gathered}`

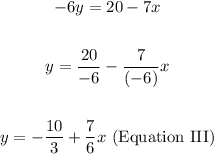
4. Substitute Equation III into the third equation and simplify:

`\begin{gathered} x+6(-(10)/(3)+(7)/(6)x)-8z=12 \\ \\ x-(60)/(3)+(7)/(6)x-8z=12 \\ \\ (13)/(6)x-8z=32 \end{gathered}`

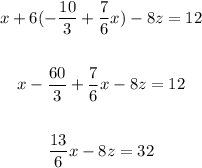
5. Substitute Equation I into the second equation and simplify: