Given the System of Equations:
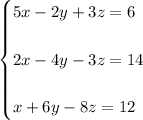
You can solve it using the Substitution Method:
1. Solve for "y" from the third equation:
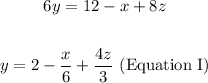
2. Add the first and the second equation:
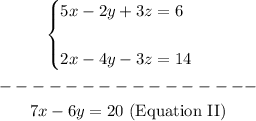
3. Solve for "y" from Equation I:
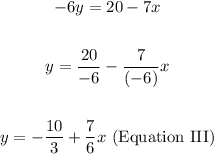
4. Substitute Equation III into the third equation and simplify:
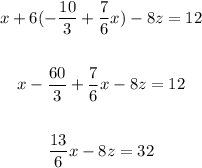
5. Substitute Equation I into the second equation and simplify:
![undefined]()