Question

A circle with center C(4,-2) passes through the point A(1,3). Does the point B (8,-2) lie inside the circle? Prove your answer

Answer 1

`\begin{gathered} (A)\Rightarrow\text{ Point B lies inside the circle Because:} \\ CA=\sqrt[]{34} \\ CB=4 \end{gathered}`

Step-by-step explanation: The general form of the equation of the circle is as follows:

`\begin{gathered} (x-x_o)^2+(y-y_o)^2=k^2 \\ (x_o,y_o)\rightarrow\text{ Center of the circle}\rightarrow(4,-2) \\ \therefore\Rightarrow \\ (x-4)^2+(y+2_{})^2=k^2\Rightarrow(1) \end{gathered}`

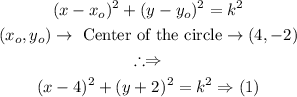
(1) is the equation of the circle. since it passes through the point (1,3), therefore substituting the (x,y) values of it in (1) gives the value complete equation (1) as follows:

`\begin{gathered} (1-4)^2+(3+2_{})^2=k^2 \\ 9+25=k^2 \\ k^2=34 \\ \therefore\Rightarrow \\ (x-4)^2+(y+2_{})^2=k^2\Rightarrow(2) \end{gathered}`

(2) is the complete equation for the circle, the following graph shows if point B is inside or outside the circle.