Question

Determine the volume of this composite objects to the nearest tenth of a cubic centimeter.

Answer 1

Based on the picture, it looks like a cylinder at the bottom part and a sphere at the top.

To solve for the volume of this composite figure, let's solve the volume of each 3D shape.

Let's start with the cylinder that has a height of 32 cm and a radius of 18 cm. The volume of the cylinder can be solved using the formula below:

The volume of the cylinder is 10, 368π cm³.

Next, let's solve the volume of the half-sphere. Here's the formula below.

`\begin{gathered} V=(4)/(3)\pi r^2 \\ V=(4)/(3)\pi(18^{3^{}}) \\ V=7,776\pi \\ Divide\text{ the volume in two because we have a half-sphere here.} \\ V=3,888\pi \end{gathered}`

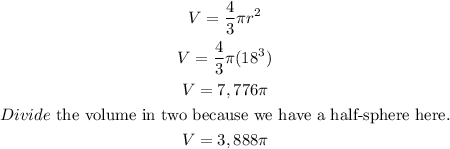
The volume of the half-sphere is 3,888π cm³.

The last step to do is add the volume of the cylinder and the half-sphere.

`\begin{gathered} V=10,368\pi+3,888\pi \\ V=14,256\pi \end{gathered}`

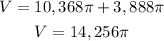
The volume of the composite figure is 14, 256π cm³.